理解快速排序的分治问题

快速排序是一个分治算法，基本思路是在每次分治中对数组A[l,r)A[l, r)找到一个分治点pp，使得pp左边的元素都小于等于A[p]A[p]，pp右边的元素都大于A[p]A[p]。注意这里与二分的不同之处在于分治算法除了要找到分治点外，还需要对数组重组。

QuickSort(A, l, r):
     if l < r :
         p = Partition(A, l, r)
         QuickSort(A, l, p - 1)
         QuickSort(A, p + 1, r)

Lomuto Partition切分算法描述如下。

注意: Lomuto Partition并不是最优的实现

将数组划分为四个部分A[l,i,j,r)A[l, i, j, r)，每个部分和目标值xx的大小关系不同，其中：

{k∈[l,i),A[k]<=xk∈[i,j),A[k]>xk∈[j,r),A[k] ? x\begin{cases} &k \in [l, i), A[k] <= x \\\\ &k \in [i, j), A[k] > x \\\\ &k \in [j, r), A[k] \ ? \ x \end{cases}

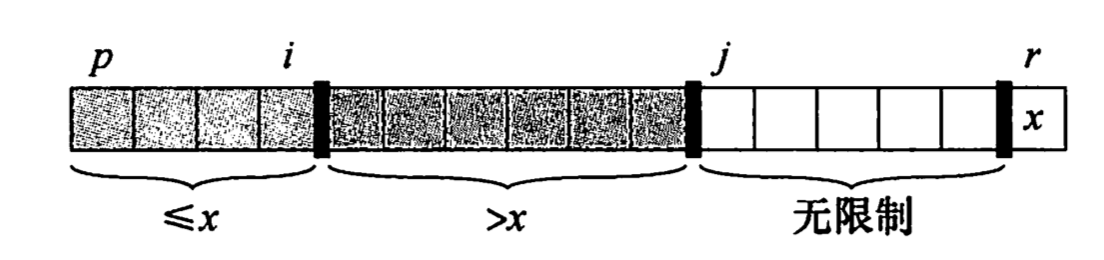
quicksort_partition.png

初始条件为i=j=l,x=A[r−1]i=j=l, x=A[r-1]，此时[l,i),[i,j)[l,i),[i,j)都为空，循环不变量成立。

终结条件为j=rj=r，此时ii即为我们要寻找的分治点。

当j=j+1j=j+1时，有两种情况：

  1. A[j]>xA[j]>x，此时对 k∈[i,j+1),A[k]>xk \in [i, j+1), A[k] > x ，不变量成立
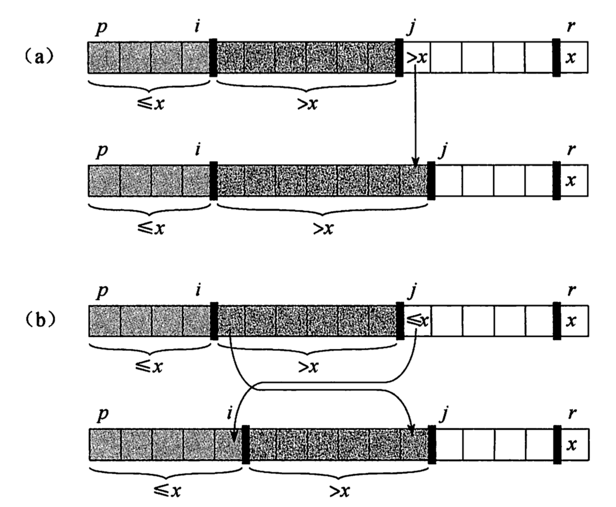
  2. A[j]<=xA[j]<=x，此时交换A[i],A[j]A[i], A[j]，i=i+1i=i+1。即把A[j]A[j]放到小于xx的区间末尾，并将此区间右移一位，保持循环不变量成立 quicksort_loop.png

按照四要素对Partition编码并实现快排。

注意：对下标的处理

func swap(A []int, i, j int) {
	tmp := A[i]
	A[i] = A[j]
	A[j] = tmp
}

func Partition(A []int, l, r int) (pivot int) {
	i := l
	j := l
	x := A[r-1]
	for j < r {
		if A[j] <= x {
			swap(A, i, j)
			i = i + 1
		}
		j = j + 1
	}
	return i - 1
}

func QSort(A []int, l, r int) {
	if l < r {
		pivot := Partition(A, l, r)
		QSort(A, l, pivot)
		QSort(A, pivot+1, r)
	}
}

分治点pp是一个有用的元素，由于它“中间点”的性质，也可以用来找第k大(小)的元素。

func KthElement(A []int, l, r, k int) int {
	if l < r {
		pivot := Partition(A, l, r)
		ki := k - 1
		if ki == pivot {
			return A[pivot]
		} else if ki < pivot {
			return KthElement(A, l, pivot, k)
		} else {
			return KthElement(A, pivot+1, r, k)
		}
	}

	return -1
}

算法导论

← Back