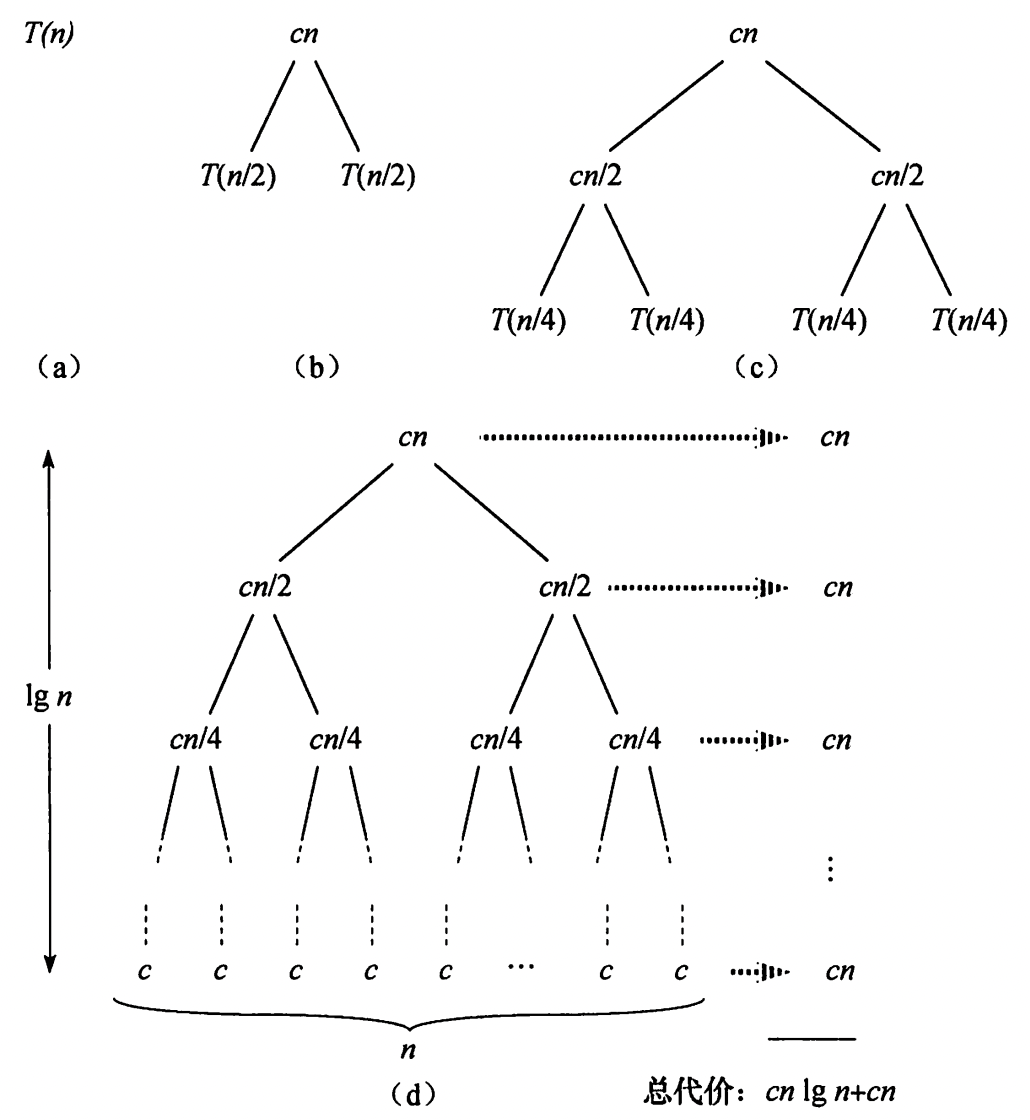
分治算法的时间复杂度

如果说没有分治，那么计算机在任何方面都不比人类高效

分治算法的思路是将原问题，拆分成若干个更小规模的子问题，并将子问题的解进行合并得到原问题的解，归并排序是使用分治算法解决的经典问题之一。

DivideAndConquer(N):
	if N eligible:
		r1 := DivideAndConquer(sub(N))
		r2 := DivideAndConquer(sub(N))
		return conquer(r1,r2) 

归并排序的流程完全对照分治算法的实现：

1. 将数组分成两半
2. 分别两个子数组进行排序
3. 将两个已排序的子数组合并

func Merge(nums, tmp []int, l, mid, r int) {
	k := l
	l1 := l
	r1 := mid
	l2 := mid + 1
	r2 := r
	for l1 <= r1 && l2 <= r2 {
		if nums[l1] < nums[l2] {
			tmp[k] = nums[l1]
			l1 = l1 + 1
		} else {
			tmp[k] = nums[l2]
			l2 = l2 + 1
		}
		k = k + 1
	}
	for l1 <= r1 {
		tmp[k] = nums[l1]
		l1 = l1 + 1
		k = k + 1
	}
	for l2 <= r2 {
		tmp[k] = nums[l2]
		l2 = l2 + 1
		k = k + 1
	}
	for l <= r {
		nums[l] = tmp[l]
		l = l + 1
	}
}

func MergeSort(nums, tmp []int, l, r int) {
	if r > l {
		mid := l + (r-l)>>1
		MergeSort(nums, tmp, l, mid)
		MergeSort(nums, tmp, mid+1, r)
		Merge(nums, tmp, l, mid, r)
	}
}

归并排序具有典型的递归子问题结构，且每次产生两个同等规模（$N$为奇数时不完全相同）的子问题，其时间复杂度的递归式如下。

$T(n)= \begin{cases} c &n=1 \\\\ 2T(n/2)+cn &n>1 \end{cases}$

大部分分治算法都有类似结构的递归式，递归式生成的递归树如图。树的总高度为$1 + lgn$，每层的复杂度为$cn$，总代价为$(1+lgn)cn$，即$nO(lgn)$。

算法导论