动态规划-切钢管

动态规划(dynamic programming)是一种分治算法，可以解决一类拥有特定性质的问题：

1. 重复子问题
2. 最优子结构

切钢管问题

GO Playground

已知长度为$i$的钢管的的售价为$p(i)$，现将长度为$n$的钢管切任意次，求所有片段的售价总和最大值及切割方案。

直观的看，对于长度为$n$的钢管可以尝试在长度$i, i \in 1,2,...,n$的位置“砍一刀”得到一根售价为$p(i)$的钢管和一个子问题$P(n-i)$，得到一个递归式。

$P(n)=Max(p(i) + P(n-i)), i \in [1,n]$

画出$P(n),n=4$的递归树，树中有多个重复子节点$P(1),P(2),P(0)$说明问题满足动态规划的性质之一重复子问题。

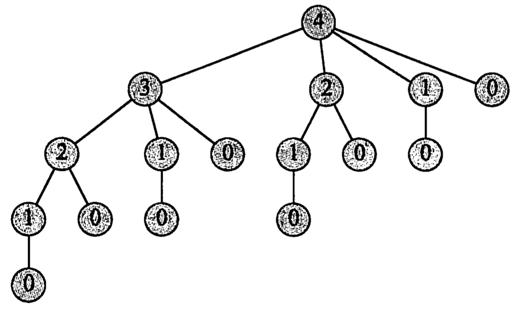
最优子结构可以通过cut-paste方法进行反证。假设$P(n)=p(i)+P(n-i)$为最优解， 而$P(n-i)$不是最优解，那么会存在另外一个$P1(n-i)$，使得$P1(n)=p(i)+P1(n-i)$为最优解，与$P(n)$为最优解矛盾。

切钢管问题简单之处在于每次切分后只会产生一个不重叠的子问题，对于一般的动态规划问题，也可以通过这种方式进行证明。确定问题的递归式和最优子结构性质后，就可以自底向上递推得出最优解。

func CuttingProblem(price []int, length int) int {
	dp := make([]int, length+1)
	for i := 1; i <= length; i++ {
		for j := 1; j <= i; j++ {
			dp[i] = max(dp[i], price[j]+dp[i-j])
		}
	}

	return dp[length]
}

动态规划中问题的最优解都是由当前问题的解和最优子问题组成，因此我们可以从后向前回溯，将所有解拼接起来得到最优解的路径。

func Path(price, cuttingPoint []int, length int) string {
	if length > 0 {
		return fmt.Sprintf("%s+%d[%d]", Path(price, cuttingPoint, length-cuttingPoint[length]), cuttingPoint[length], price[cuttingPoint[length]])
	}
	return ""
}

func CuttingProblem(price []int, length int) int {
	dp := make([]int, length+1)
	cuttingPoint := make([]int, length+1)
	for i := 1; i <= length; i++ {
		for j := 1; j <= i; j++ {
			if price[j]+dp[i-j] > dp[i] {
				dp[i] = price[j] + dp[i-j]
				cuttingPoint[i] = j
			}
		}
	}

	fmt.Println(Path(price, cuttingPoint, length))

	return dp[length]
}

Reference

• 算法导论